2 МАШИННЫЙ РАСЧЕТ СТАЦИОНАРНОГО РЕЖИМА ЗАДАННОЙ ЭНЕРГОСИСТЕМЫ НА ОСНОВЕ МАТРИЧНЫХ УРАВНЕНИЙ
Расчет стационарного режима производится методом узловых напряжений (МУН), методом контурных токов (МКТ) или на основе законов Ома и Кирхгофа. Рассмотрим эти методы.
2.1 Алгоритм программы с методом узловых напряжений
Этот метод является частным случаем метода независимых напряжений. При этом матрица узловых проводимостей симметрична, и для цепей без взаимоиндукции ее можно сформировать прямо по заданной схеме. При наличии взаимных индуктивностей между ветвями схемы, эту матрицу надо находить путем обращения квадратной матрицы сопротивлений ветвей Zv, состоящей из собственных и взаимных сопротивлений ветвей.
Основное матрично-векторное уравнение этого метода имеет вид:
![]()
где ![]() - (q-1)-мерный вектор искомых узловых напряжений (q – общее количество узлов схемы);
- (q-1)-мерный вектор искомых узловых напряжений (q – общее количество узлов схемы);
![]() - квадратная (q-1)-порядка матрица узловых проводимостей схемы;
- квадратная (q-1)-порядка матрица узловых проводимостей схемы;
![]() - (q-1)-мерный вектор источников тока, подключенных к узлам схемы;
- (q-1)-мерный вектор источников тока, подключенных к узлам схемы;
![]() - (q-1)-мерный вектор эквивалентных источников тока, полученных в результате замены ЭДС ветвей на источники тока.
- (q-1)-мерный вектор эквивалентных источников тока, полученных в результате замены ЭДС ветвей на источники тока.
Приведенные выше величины рассчитываем по формулам:
![]()
![]()
![]()
![]()
где ![]() - матрица проводимостей ветвей (
- матрица проводимостей ветвей (![]() );
); ![]() - матрица узловых проводимостей, используемая для преобразований ЭДС ветвей в эквивалентные источники тока;
- матрица узловых проводимостей, используемая для преобразований ЭДС ветвей в эквивалентные источники тока; ![]() - вектор напряжений ветвей;
- вектор напряжений ветвей; ![]() - вектор токов ветвей.
- вектор токов ветвей.
![]()
Мощности ветвей определяем как ![]()
Рассмотрим программы, реализующие изложенный выше алгоритм при линейном и нелинейном способе задания нагрузок энергосистемы.
2.1.1 Метод узловых напряжений в линейном варианте (сопротивления всех нагрузок принимаем постоянными)
Формируем вектор сопротивлений ветвей V_param всей схемы. Очередность расположения ветвей принимаем такой, как указано ниже:

Программа формирования вектора сопротивлений Vzv приведена ниже. В ней используется матрица V_param, которая состоит из 5-ти матриц.
![]()

Для нашего примера
![]()
![]()
![]()
![]()
![]()

Формируем теперь матрицу проводимостей ветвей Yv с учетом взаимоиндукции между 1 и 2 ЛЭП. Матрица будет квадратной и состоять из собственных и взаимных сопротивлений:
![]()
![]()
![]()
![]()
![]()
Формируем вектор ЭДС ветвей схемы, в котором используются ЭДС генераторов из 5-го столбца матрицы Gen.
:
![]()
![]()
![]()
![]()
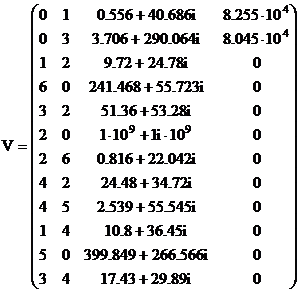
Формируем матрицу V для всей схемы, в которой объединены матрицы V1, матрица собственных сопротивлений ветвей Vzv и матрица ЭДС Е
![]()
![]()
![]()
Здесь обозначены векторы N и K как векторы начальных и конечных узлов, к которым подключена ветвь.
Формируем вектора межузловых источников тока (ток считаем положительным, если он подходит к узлу). У нас источник тока один– третья нагрузка.
![]()
![]()
![]()
![]()
Сформируем матрицу соединений P –матрицу связей ветвей с узлами. .В схеме всего 7 узлов и 12 ветвей. Программа формирования этой матрицы приведена ниже.

![]()

Матрицу Р разобьём на две подматрицы Р1(связи хорд с узлами) и Р2(связи ветвей дерева с узлами).Надо иметь в виду, что число хорд равно числу ветвей минус число узлов(без базисного). В нашем примере число хорд будет равно 11-6 =5, а число ветвей дерева равно числу узлов схемы(без базисного).т.е.7-1=6
![]()
![]()


Используя формулы МУН:
![]()
![]()
![]()
![]()
находим узловые напряжения (фазные), токи и напряжения ветвей:
![]()
 кВ
кВ
Напряжения ветвей: Токи ветвей:
![]()
![]()
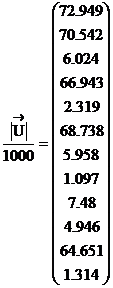 кВ
кВ 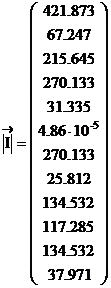 А
А
Выполним расчет мощностей: ![]()
![]()
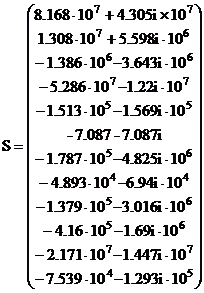 ВА
ВА
![]() ВА
ВА
2.1.2 Метод узловых напряжений в нелинейном варианте.
Формируем диагональную матрицу собственных сопротивлений ветвей с учетом нелинейностей нагрузок, которые должны быть учтены здесь как функции узловых напряжений. В нашем примере нелинейные нагрузки 1 и 2. Программа приведена ниже.
![]()
![]()
![]()

Программа расчета узловых напряжений с учетом нелинейности нагрузок:

![]()
![]()
![]()
![]()
Результат расчета и его сравнение с линейным вариантом (в относительных и именован ных единицах):
ных единицах):


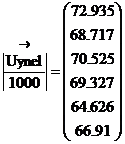 кВ
кВ  кВ
кВ
Сопротивления нагрузок:
![]() Ом
Ом
![]() Ом
Ом
![]() Ом
Ом
![]() Ом
Ом
Напряжения ветвей: Токи ветвей:
![]()
![]()
 кВ
кВ  А
А
Построение векторных диаграмм(ВД) узловых напряжений:

Построение ВД напряжений и токов в узле:
![]()
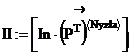
![]()
![]()
![]()
![]()
![]()
![]()

Произведем расчет мощностей:
![]()
![]()
![]()
![]()
![]() ВА
ВА ![]() ВА
ВА
I закон Кирхгофа:
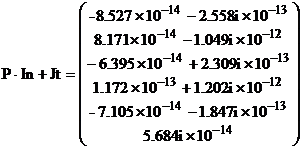
Матрица S -матрица мощностей ветвей.
 ВА
ВА
Видим, что активные мощности ветвей, в которых находятся ЭДС, положительны, а остальные ветви содержат отрицательные значения, т.е. потребляют мощность.
Произведем расчет потерь мощности в сети:
Определяем генерируемую активную мощность Pg:
![]()
![]() Вт
Вт
Определяем мощность, потребляемую нагрузками
![]()
![]() Вт
Вт
В процентах определяем потери мощности на передачу электроэнергии (то есть потери в линиях и трансформаторах):
![]()
![]() %
%
2.2 Алгоритм программы с методом контурных токов
Основное матрично-векторное уравнение этого метода имеет вид:
![]()
где ![]() - n-мерный вектор искомых контурных токов;
- n-мерный вектор искомых контурных токов;
![]() - квадратная порядка n матрица контурных и взаимных сопротивлений, формируемая как:
- квадратная порядка n матрица контурных и взаимных сопротивлений, формируемая как:
![]() ,
,
где ![]() ,
, ![]() - исходная и транспонированная матрицы независимых контуров (ветви-контуры);
- исходная и транспонированная матрицы независимых контуров (ветви-контуры);
![]() - матрица сопротивлений ветвей;
- матрица сопротивлений ветвей;
![]() - вектор контурных ЭДС, имеющий размерность n и определяемый через ЭДС ветвей Е как:
- вектор контурных ЭДС, имеющий размерность n и определяемый через ЭДС ветвей Е как:
![]()
![]() - вектор эквивалентных контурных ЭДС, создаваемых заданными в узлах схемы источниками тока:
- вектор эквивалентных контурных ЭДС, создаваемых заданными в узлах схемы источниками тока:
![]()
где ![]() - квадратичная размерности n´n матрица сопротивлений для источников тока, вычисляемая как:
- квадратичная размерности n´n матрица сопротивлений для источников тока, вычисляемая как:
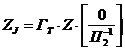
![]() - обратная матрица от матрицы соединений узлов и ветвей дерева схемы.
- обратная матрица от матрицы соединений узлов и ветвей дерева схемы.
Тогда уравнение метода контурных токов примет вид:
 (1)
(1)
Из уравнения (1) можно найти вектор контурных токов, но для этого надо сформировать для ветвей схемы векторы ЭДС, токов, матрицы сопротивлений, матрицы соединений П, независимых контуров Г, а также векторы задающих источников токов в узлах схемы ![]() .
.
Решив уравнение (1), находим контурные токи ![]() , после чего вычисляем вектор токов всех ветвей как:
, после чего вычисляем вектор токов всех ветвей как:
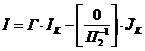
напряжения ветвей как:
![]()
мощности ветвей как:
![]()
где ![]() - вектор сопряженных комплексов токов ветвей.
- вектор сопряженных комплексов токов ветвей.
2.2.1 Расчет методом контурных токов без учета нелинейности нагрузок
Найдем матрицу Bi главных контуров, которым соответствуют хорды, а также матрицу контуров Bij для источников тока:
![]()
![]()
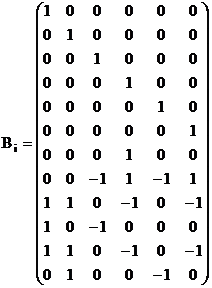

Находим матрицу контурных сопротивлений Zk:
![]()
Находим матрицу контурных сопротивлений для источников тока Zj:
![]()
Находим вектор контурных ЭДС Eке:
![]()
Заменяем источники тока эквивалентными контурными ЭДС Eкj:
![]()
Находим вектор контурных токов Ikont:
![]()
Находим вектор токов ветвей Iv:
![]()
Напряжения ветвей находим, используя закон Ома:
![]()
Напряжения в узлах рассчитываем по формуле:
![]()
Сравним результаты расчетов разными методами для линейных нагрузок:
МКТ МУП
 кВ
кВ  кВ
кВ
Для проверки правильности решения выполним проверку по первому и второму законам Кирхгофа:
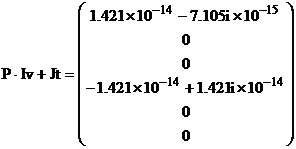
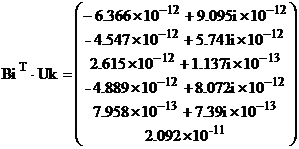
2.2.2 Расчет методом контурных токов с учетом нелинейности нагрузок
В исходных данных первая нагрузка задана нелинейной как функция от напряжения. При использовании метода МКТ, она должна быть представлена как функция от тока. Поэтому в программе расчета нелинейная зависимость сопротивления первой нагрузки от тока Znn1(I) находится из решения методом итераций уравнения (находим напряжение, которое соответствует заданному току):
U-Z(U)*I=0
Решение этого уравнения можно получить одним из двух методов:
а) с помощью функции root , имеющейся в MATHCAD:
![]()
![]()
![]() Ом
Ом
б) с помощью приведенной ниже программы (метод итераций):

![]() Ом
Ом
Формируем диагональную матрицу собственных сопротивлений ветвей с учетом нелинейностей нагрузок и матрицу взаимных сопротивлений (ZZ).

Определяем контурные токи:
![]()

![]()
Находим токи ветвей схемы:
![]()
Находим напряжения ветвей схемы:
![]()
Находим напряжения в узлах схемы:
![]()
Сравниваем результаты расчетов различными методами:
МКТ в нелинейном МУП в нелинейном МУП в линейном
варианте: варианте: варианте:
 кВ
кВ 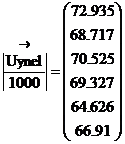 кВ
кВ  кВ
кВ
2.3 Метод и программа расчета токов и напряжений в схеме на основе уравнений законов Ома и Кирхгофа в матричной форме
Сформируем и решим записанное в матричном виде уравнение указанных законов:
 Откуда найдем
Откуда найдем 
где:![]() - нулевая матрица
- нулевая матрица ![]() размером как матрица P
размером как матрица P
![]() - нулевая матрица
- нулевая матрица ![]() размером как матрица
размером как матрица ![]()
![]() -вектор
-вектор ![]() с размерностью равной числу хорд
с размерностью равной числу хорд
![]() - диагональная единичная
- диагональная единичная ![]() матрица с размером числа ветвей
матрица с размером числа ветвей
Матрицы блочного уравнения:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Сравним полученные результаты с линейным вариантом МУП:
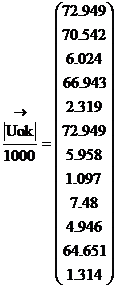 кВ
кВ 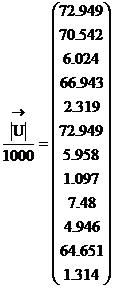 кВ
кВ
 А
А 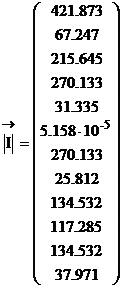 А
А
Таким образом, линейные варианты расчетов полностью совпадают между собой.
2.4 Выбор емкостей для компенсации реактивной мощности нагрузок и оценка экономической эффективности этого метода
2.5.1 Расчет емкостей в узлах подключения первой и второй нагрузок
Начальные значения требуемых емкостей найдем по формуле:
![]()
которая получена из условия, что индуктивная проводимость нагрузки будет равна ёмкостной проводимости конденсаторов.
С учетом изложенного, имеем:
![]()
![]()
![]()
В связи с тем, что при подключении ёмкостей напряжения в узлах схемы возрастут и изменятся реактивные мощности нагрузок и конденсаторов, необходимо начальные значения ёмкостей уточнить. Это связано с тем, что сопротивления нагрузок нелинейные и зависят от уровня напряжений в узле, тогда как сопротивления ёмкостей не зависят от напряжения. Уточнения будем выполнять с помощью приведенной ниже программы.
Программа для расчета сопротивлений нагрузок с учетом емкостей, а также для расчета значений токов и напряжений после установки компенсирующих устройств, приведена ниже. В ней учитывается одновременное влияние ёмкостей, устанавливаемых в обоих узлах нагрузки. Расчет установившегося режима производится методом узловых напряжений с пошаговым уточнением методом простых итераций:

![]()
![]()
![]()
![]()
![]()
![]()
![]() Ом
Ом
![]() Ом
Ом
Емкости конденсаторных батарей:
до оптимизации: после оптимизации:
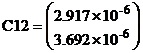 Ф
Ф  Ф
Ф
Находим искомые значения токов и напряжений:
 кВ
кВ  А
А
Значения узловых напряжений:
С установкой компенсирующих устройств Без установки компенсирующих устройств
 кВ
кВ  кВ
кВ
Произведем расчет мощностей:
![]()
![]()
![]() ВА
ВА
![]()
![]()
![]() ВА
ВА
Баланс мощностей:
![]() ВА
ВА
Произведем проверку по I закон Кирхгофа :
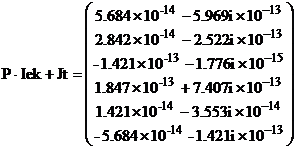
Определяем генерируемую активную мощность с учетом установленных компенсирующих устройств Pg_ek:
![]()
Генерируемая мощность составляет:
![]() Вт
Вт
Определяем мощность потребляемую нагрузками Pn_ek с учетом установленных компенсирующих устройств:
![]()
![]() Вт
Вт
В процентах определяем потери мощности на передачу.(то есть потери в линиях и трансформаторах)
![]()
![]()
Определяем экономию EK в процентах.(то есть на сколько снизились потери мощности за счет установки компенсирующих устройств)
![]()
![]()
Найдем мощность сэкономленных потерь
![]() или
или ![]() Вт
Вт
Определяем количество выработанной за год электроэнергии W, зная:
число часов работы генераторов Т, которое примем равным 6600.
![]()
![]()
![]() кВтч
кВтч ![]() кг
кг
Принимая, что на выработку одного киловаттчаса расходуется q=0.4 килограмм угля рассчитываем экономию угля:
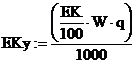
![]() тонн
тонн
Принимая что одна тонна угля стоит 150 гривен, рассчитываем экономию средств Ekгрн:
![]()
![]() грн/год
грн/год
Стоимость установленных конденсаторов емкостью 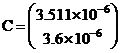 Ф
Ф
на напряжение Uvn=110 кв по справочным данным составляет 300 тыс.гривен.
Тогда срок окупаемости составит:
![]()
![]()
![]() год
год
![]()
![]()
То есть срок окупаемости составит 18 месяцев, что очень эффективно.