ОБЩИЕ ПРИНЦИПЫ РАСЧЕТА НАДЕЖНОСТИ
ОЦЕНКА НАДЕЖНОСТИ ЭЛЕКТРОСЕТЕВЫХ КОНСТРУКЦИЙ
Как самостоятельный раздел науки теория надежности сформировалась к концу 50-х годов, в первую очередь, под влиянием развития радиоэлектроники, вычислительной и ракетной техники. Тогда отечественная школа теории надежности, руководимая академиком АН УССР Б. В. Гнеденко, заняла одно из ведущих мест в мире.
Первые отдельные статьи, посвященные оценке надежности систем энергетики, появились еще в середине 30-х годов. Наиболее интенсивно задачи оценки и обеспечения надежности начали решаться в начале 40-х годов, что было вызвано разработкой сложных электронных систем, предназначенных для военных целей. Однако впервые проблемы теории надежности были сформулированы строительной механикой. Теория надежности строительных конструкций развивалась независимо от теорий надежности в машиностроении и энергетике. Лишь в последние годы происходит интенсивный взаимный обмен результатами.
Специфика теории надежности строительных конструкций состоит в том, что необходимо учитывать совместное действие случайных нагрузок на систему со случайными прочностными характеристиками. По мере развития теории надежности предлагались различные способы оценки надежности строительных конструкций.
ОБЩИЕ ПОЛОЖЕНИЯ
В настоящее время расчет несущих строительных конструкций производится по методу предельных состояний. При этом общая надежность конструкций не нормируется и считается, что необходимый уровень надежности обеспечивается при выполнении требований действующих нормативных документов. Вероятностная природа и изменение физико-механических свойств конструкции с течением времени не учитывается. Предполагается, что коррозионный износ элементов конструкции исключен благодаря использованию определенных мер защиты, а старение материала незначительно. Подобное положение объясняется, с одной стороны, отсутствием достаточно обоснованных и практически приемлемых стохастических методов расчета конструкций, с другой,— нехваткой статистических данных о свойствах проектируемых объектов, воспринимаемых ими нагрузках, а также недостатком информации
о фактической надежности существующих сооружений.
Это приводит к необоснованному увеличению надежности малоответственных конструкций с небольшим сроком эксплуатации и конструкций, воспринимающих большое число нагрузок при малой вероятности их сочетания с одновременным достижением максимальных значений. В то же время одинаковые по функциональному назначению, но запроектированные для различных условий эксплуатации конструкции имеют неодинаковые уровни надежности.
Обычный детерминистский подход, используемый при расчете строительных конструкций по методу допускаемых напряжений или разрушающих нагрузок, и «полувероятностный» подход, применяемый в методе расчета по предельным состояниям, включают два этапа. На первом этапе вычисляются напряжения, деформации и перемещения в конструкциях под действием внешних нагрузок или вычисляются некоторые предельные значения этих нагрузок. Для решения этих задач используют методы строительной механики, теории упругости, пластичности и пр. Второй этап расчета состоит в сопоставлении вычисленных напряжений, деформаций и перемещений с некоторыми предельно допустимыми (нормативными) значениями либо в сопоставлении расчетных и предельных нагрузок.
Будучи элементарным, второй этап расчета является в то же время весьма важным. Именно на этом этапе косвенными и сравнительно примитивными методами выбирается достаточно надежная, долговечная и экономичная конструкция.
Надежность является комплексным свойством системы (или отдельного ее элемента) и характеризуется способностью системы функционировать в течение заданного времени в определенных условиях при сохранении своих рабочих параметров в пределах, установленных в технической документации. Другими словами, надежность — устойчивость качества системы по отношению ко всем возможным возмущениям, встречающимся на любых этапах ее существования.
Такое определение выдвигает ряд проблем. Необходимо четко установить условия и особенности функционирования, количество выполняемых функций и объем профилактического обслуживания, определить границы допустимых изменений характеристик объекта, параметры которого неизбежно ухудшаются с течением времени и т.п.
В связи с тем, что «надежность» невозможно формализовать существующими математическими методами, на практике производят расчет целого ряда характеристик, которые называют показателями надежности. В теории и практике анализа надежности электроэнергетических и механических систем накоплен значительный опыт формализации таких характеристик, описывающих различные свойства объекта.
Комплекс показателей надежности включает пять групп: показатели безотказности, ремонтопригодности, долговечности, экономические показатели, комплексные показатели. Причем в зависимости от конкретных целей и задач (проектирование и расчет, выполнение экспертных оценок, теоретические исследования и пр.) выбирается определенная группа критериев. Для оценки надежности конструкций электросетевого строительства наиболее часто используют вероятность безотказной работы.
Разработка методов оценки надежности систем и создания систем, обладающих заданными показателями надежности и долговечности, составляет содержание теории надежности и базируется на математическом аппарате теории вероятностей и математической статистики.
Строго говоря, в ряде работ, посвященных этой проблематике, проводится четкая грань между собственно теорией надежности и статистической динамикой конструкций. При этом считается, что теория надежности занимается исключительно вопросами обеспечения требуемой надежности для различных систем, а статистическая динамика исследует поведение сооружений при случайных внешних воздействиях, т.е. устанавливает связи между входными и выходными параметрами системы в случае, если внешние воздействия и поведение системы являются случайными. В зависимости от того, какие параметры являются заданными, а какие — искомыми, различают четыре типа задач статистической динамики.
Первая (основная) задача состоит в нахождении характеристик выходных параметров при заданных характеристиках входных параметров и параметров системы. Вторая задача является обратной первой и заключается в нахождении характеристик входных параметров, когда известны свойства системы и выходные параметры. Третья, задача заключается в определении свойств стохастической системы по известным характеристикам на ее входе и выходе. Четвертая задача статистической динамики сводится к отысканию системы, которая при заданных внешних воздействиях обладает заданными свойствами. Иначе говоря, синтезируется оптимальная система.
Среди методов решения задач статистической динамики широкое распространение получили методы функций Грина, дифференциальных уравнений, спектральных представлений (метод преобразований Фурье), использования теории марковских процессов и др.
Статистическая динамика и теория надежности конструкций тесно связаны между собой. При решении конкретных задач методы этих двух разделов строительной механики обычно применяют последовательно. Поэтому в дальнейшем при рассмотрении поведения сооружений и установления их предельных состояний граница между статистической динамикой и теорией надежности проводиться не будет.
Исследование надежности методами теории вероятностей, безусловно, приводит к тому, чтобы оценивать надежность, в первую очередь, через вероятность. При этом считают, что система (или ее элемент) может находиться только в двух состояниях: отказа (К) или безотказной работы (F). Обоим состояниям соответствуют определенные вероятности. Эта предпосылка несколько упрощает оценку показателей надежности, позволяя исключить из рассмотрения качество передаваемой электроэнергии (например, преднамеренные отключения с целью профилактики в число отказов не включаются).
Вероятность отказа (выхода из строя) Pf = P(V') — вероятность того, что в рассматриваемом интервале времени Т будет превзойдено предельное состояние и таким образом будет достигнуто состояние отказа. Вероятность безотказной работы (вероятность выживания) Ps = Р (V) — вероятность того, что за время Т не будет выхода за предельное состояние.
Событие V противоположно событию V:
Ps + Pf= 1. (1)
Часто в строительстве рассматривается вероятность отказа, а не вероятность безотказной работы, так как это нагляднее и имеет преимущества в численной оценке.
В общем случае существуют различные методы определения вероятности отказа. Можно оценивать ее на основе статистического анализа повреждений и определения частоты отказов как приближения к вероятности отказов. Так поступают в электронике при оценке событий малой длительности. Однако в электросетевом строительстве такой путь исключен по нескольким причинам.
- Строительные сооружения являются системами с большой надежностью, их выход из строя — редкое событие и в связи с этим вероятность отказа мала. Для ее статистической оценки необходим столь большой объем выборки, которого на практике невозможно достигнуть. И хотя в настоящее время все основные типы унифицированных опор и порталов проходят механические испытания на полигонах, цель таких испытаний состоит в подтверждении того, что конструкция способна выдержать расчетную нагрузку с определенным запасом. Получить характеристики надежности в результате таких испытаний невозможно, так как для этого необходимо довести до разрушения большое число конструкций, а это экономически не целесообразно. Кроме того, не разработана методология проведения эксперимента, позволяющая прогнозировать надежность конструкции.
- Число однотипных сооружений и конструкций недостаточно. Велико разнообразие конструктивных форм, часто встречаются сооружения, не имеющие аналогов. В таких случаях единая основа для сбора статистической информации отсутствует. Конечно, в общем объеме электросетевых конструкций можно выделить группы однотипных элементов и конструкций и создать единую основу для сбора информации об отказах. Но количественно оценить надежность сооружения по этим данным едва ли возможно, ведь даже типовые конструкции, расположенные в одном климатическом районе, не являются абсолютно идентичными, так как воспринимают различные нагрузки и воздействия (например, из-за различных пролетов или стрел провеса провода, различной массы технологического оборудования и пр.).
- Сроки службы сооружений велики. Даже если и можно сделать приемлемые выводы на основе статистики повреждений, эти выводы появятся лишь тогда, когда они, в лучшем случае, будут представлять исторический интерес.
Тем не менее даже для уникальных сооружений характеристики надежности могут быть определены на основе свойств конструкции и окружающей среды, носящих массовый характер и оцениваемых статически. К этим свойствам относятся свойства строительных материалов, производимых и испытываемых как массовые продукты, внешние нагрузки, которые часто повторяются и могут наблюдаться и оцениваться, геометрические размеры элементов и сооружения в целом, характеристики соединений и стыков, свойства грунтов и т.д. Все эти параметры в теории, надежности определяются как базисные переменные X1, Х2, Хт. Они могут быть представлены математически как случайные величины или стохастические процессы и найдены на основе статистических исследований. Тогда предельное состояние конструкции определяется как функция базисных переменных.
В общем случае для решения основной задачи теории надежности несущих строительных конструкций, т.е. для теоретического определения вероятности наступления состояния отказа, необходима следующая исходная информация:
- исчерпывающие статистические данные о базисных переменных Xt;
- математическая модель, определяющая взаимосвязь между внешними нагрузками и воздействиями и внутренними усилиями (напряжениями) в элементах конструкции;
- определено предельное состояние, для которого вычисляется вероятность отказа;
- достаточно простой математический аппарат для обработки случайных чисел и стохастических процессов.
Многие исследователи в области теории надежности считают, что достичь исчерпывающих знаний о распределении базисных переменных практически невозможно. С одной стороны, для установления с достаточной достоверностью типа распределений требуется большой объем выборок, в особенности для зон на «хвостах» кривых распределений, получить который на практике часто невозможно. С другой стороны, именно эти «хвосты» и оказывают решающее влияние на значение вероятности отказа. В связи с этим высказываются сомнения по поводу того, может ли вероятность отказа служить мерой надежности конструкции и может ли она быть определена с достаточной степенью достоверности.
Дискуссия по этому вопросу привела к появлению двух подходов к решению задач теории надежности. Первое направление исходит из того, что при приемлемых затратах времени всегда можно найти первые два момента распределения (математическое ожидание и стандартное отклонение), а также ковариации на основе методов оценок, оптимальным образом использующих статистическую информацию. В этом случае определить вероятность отказа невозможно, можно найти лишь индекс безопасности, являющийся мерой надежности системы. Рассмотренный метод оценки надежности получил название метода моментов.
Второе направление основывается на предположении об исчерпывающем знании о базисных переменных и принимает вероятность отказа как меру надежности и как прогноз относительной частоты отказов для однотипных конструкций.
При теоретическом определении вероятности находят только ту ее часть, которая зависит от базисных переменных. Это теоретическое значение, естественно, не учитывает не поддающийся статистическому описанию человеческий фактор (ошибки проектирования, изготовления, монтажа, эксплуатации и пр.). Кроме того, на численное значение теоретической вероятности отказа определенное влияние оказывают несовершенства механической модели конструкции (сооружения). Поэтому теоретическая вероятность отказа может оказаться ниже фактической вероятности. При выборе же механической модели, дающей запас прочности, напротив, расчетная вероятность отказа будет завышена.
Важен и другой аспект. Теоретически найденная вероятность отказа весьма чувствительна к изменениям стохастической модели. С помощью статистических исследований можно достаточно точно оценить среднюю часть кривой плотности распределения, а также среднее и стандартное отклонение. Однако поведение кривой распределения в области редких событий нельзя обосновать статистически. В этом случае исходные предпосылки и гипотезы очень сильно влияют на результат, особенно на малые значения вероятностей, а именно с такими значениями и приходится иметь дело.
Вероятность отказа сооружения, вычисляемая теоретически, является условной (оперативной) вероятностью, действительной только при выполнении целого комплекса предположений, например о типах распределений базисных переменных, о соответствии механической модели сооружения его реальной работе и т.д. Эта величина связана с теоретической моделью и не может быть отделена от нее. Впрочем, несовершенство оперативной вероятности отказа будет несущественно, если она понимается не как действительное значение надежности, а как количественный критерий для принятия решений при проектировании или оценке технического состояния эксплуатируемых конструкций.
Оперативная вероятность отказа не учитывает ошибочных действий человека, трудно поддающихся оценке на всех стадиях строительства и эксплуатации. Однако задачу упрощает то обстоятельство, что, с одной стороны, ошибочные действия человека мало влияют на надежность конструкции, а с другой, — они не зависят от выбора параметров конструкции и едва ли оказывают влияние на назначение экономически оптимальных параметров.
Вероятность отказа является функцией времени. Это связано, в первую очередь, с зависимостью нагрузок и воздействий, а также свойств материалов от времени. Чем больше период времени, к которому относится вероятность отказа, тем больше вероятность того, что состояние отказа будет достигнуто. Таким образом, Pf — возрастающая функция времени, при t1 < t2 — Pf (fx) < Pf (t2).
Если предположить, что сооружение в начальный момент своего существования находится в состоянии безотказной работы, то имеют место два граничных значения:
![]() (2)
(2)
Сказанное означает, что теория надежности должна учитывать зависимость вероятности отказа от времени. Реальные строительные конструкции выполнены из материалов, свойства которых с течением времени изменяются. Все материалы подвержены процессам старения, усталости, упрочнения, коррозии, ползучести и другим зависящим от времени явлениям, которые изменяют несущую способность, как правило, в сторону уменьшения. Эти явления существенно влияют на вероятность отказа. Но даже при часто принимаемых упрощенных предположениях о независимости свойств материалов от времени в исследованиях надежности нельзя не учитывать зависимость нагрузок от времени.
Использовать вероятность отказа как меру надежности можно только в том случае, когда будет назначен период времени, для которого эта вероятность определена. В качестве такого периода времени целесообразно выбрать срок службы сооружения. Существуют и другие точки зрения относительно длительности этого периода. Например, предлагается в качестве временного интервала, используемого при оценке вероятности отказа, выбрать период длительностью один год. Выбор отрезка времени, для которого определяется вероятность, зависит, в первую очередь, от решаемой задачи.
Вероятность безотказной работы содержит в себе значительную информацию о надежности системы. Через эту величину могут быть выражены другие показатели надежности и долговечности. К ним относится, в частности, срок существования сооружения.
Под сроком существования Т понимают время от начала эксплуатации до наступления отказа. Срок существования сооружения — величина случайная и характеризуется плотностью и функцией распределения.
Функцией распределения F(x) называют функцию, текущее значение которой равно вероятности того, что случайная величина Т не превзойдет произвольного значения t:
![]() (3)
(3)
Плотностью распределения вероятностей называют первую производную от функции распределения
![]() (4)
(4)
Функция распределения сроков существования FT (/) равна вероятности того, что срок существования Т меньше либо равен V.
![]() (5)
(5)
Плотность распределения сроков существования
![]() (6)
(6)
Если известны функции FT (f) или fT (I) легко получить среднюю продолжительность существования сооружения (среднюю наработку до отказа):
![]() (7)
(7)
Из формулы (7) видно, что срок существования и вероятность отказа взаимосвязаны. Поэтому надежность сооружения может быть оценена как с помощью вероятности отказа, так и с помощью срока существования. Срок существования тесно связан со сроком службы — периодом времени предполагаемой эксплуатации сооружения, для которого должна быть гарантирована заданная надежность и безопасность. Срок службы является планируемой величиной, имеющей постоянное значение.
В строительной практике удобнее оперировать понятием «срок существования сооружения». Однако в связи с более простым определением вероятности отказа чаще используют именно эту характеристику.
Характеристикой надежности во времени для невосстанавливаемых объектов может служить интенсивность потока отказов — условная плотность вероятности отказа для сооружения, достигшего возраста t.
Мгновенное значение интенсивности отказов определяется как предел отношения вероятности отказа в интервале времени к величине этого интервала при Д t,стремящемся к нулю:
![]() . (8)
. (8)
Очевидно, что интенсивность потока отказов имеет размерность.
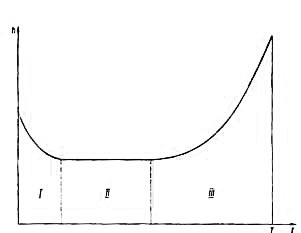
Рис. 2 1. Зависимость интенсивности отказов от времени
Зависимость интенсивности отказов от времени практически всегда имеет три характерные области (рис. 1). В начале эксплуатации многократно встречаются выбросы (область I). В электросетевых конструкциях это большей частью связано с низким качеством работ и материалов. На следующем этапе жизни сооружения (область 2) интенсивность отказов относительно постоянна. Здесь чаще всего отказы вызваны перегрузками и непредвиденными внешними воздействиями. Завершающий этап существования (область 3) характеризуется ростом интенсивности отказов, связанным с уменьшением несущей способности конструкции вследствие процессов коррозии, усталости и пр.
Для восстанавливаемых объектов характеристикой надежности во времени служит частота отказов (параметр потока отказов) со (t) — величина, равная количеству отказов в единицу времени:
![]() (9)
(9)
где E[n(t)] — математическое ожидание количества отказов за время /; Е [п (t + A t)] — то же за время 1 + A t.
Вероятность отказа Рр вероятность безотказной работы Ps, плотность распределения, срока существования сооружения и интенсивность отказов h являются функциями, которые полностью характеризуют изменение надежности во времени. Все эти функции взаимосвязаны (табл. 1).
Помимо показателей безотказности для оценки надежности электросетевых конструкций используют показатели ремонтопригодности и долговечности.
Под ремонтопригодностью понимают приспособленность системы к предупреждению отказов и восстановлению работоспособного состояния при проведении необходимого технического обслуживания и ремонтов.
2.1. Взаимозависимость различных характеристик надежности
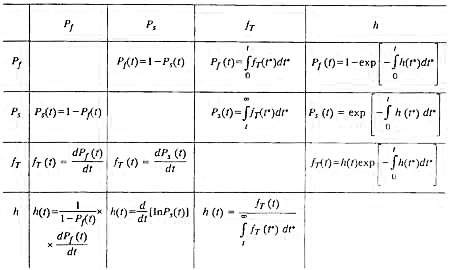
Ремонтопригодность воздушной линии и открытых распределительных устройств характеризуется затратами времени, средств, а также эффективностью ремонтов и оценивается следующими показателями:
- средним временем восстановления при отказе;
- средней продолжительностью преднамеренного отключения BЛ или ОРУ для проведения технического обслуживания;
- средней периодичностью преднамеренных отключений;
- средними трудозатратами на капитальный ремонт и техническое обслуживание.
Долговечность — свойство сохранять работоспособность при установленной системе ремонтов и технического обслуживания. В соответствии с ГОСТ 27.002—83 в качестве показателя долговечности может быть принят полный средний срок службы, т.е. календарная продолжительность эксплуатации, при достижении которой дальнейшая работа ВЛ или ОРУ технически невозможна или экономически нецелесообразна.
Этот показатель определяется большим числом факторов, связанных с конструктивными особенностями сооружений и результатами взаимодействия с окружающей средой. Средний срок службы ВЛ электропередачи и ОРУ в целом определяется сроками службы отдельных элементов — опор, порталов, проводов, изоляторов, электрического оборудования,— закономерности износа и старения которых изучаются для оценки оптимального срока службы ВЛ и ОРУ. В СССР срок службы ВЛ 35—750 кВ до списания определялся как величина обратная амортизационным отчислениям на реновацию и для линий на металлических и железобетонных опорах обычно составлял 50 лет. Государственные строительные нормы Украины устанавливают срок службы опор ВЛ равный 40 годам. Однако дефицит материальных или трудовых ресурсов часто вынуждает продолжать эксплуатацию конструкций, когда экономически целесообразна их замена.
Комплексные показатели надежности характеризуют несколько свойств системы: безотказность, долговечность, ремонтопригодность.
Важнейшим комплексным показателем воздушной линии электропередачи является коэффициент ее технического использования:
![]() (10)
(10)
где Т — среднее время работы ВЛ между отказами (наработка на отказ); Тв — среднее время восстановления ВЛ; Тр — средняя продолжительность преднамеренных отключений ВЛ.
Часто используют и другие комплексные показатели — коэффициенты готовности, простоя, простоя при преднамеренных отключениях
.
Наиболее часто используемым экономическим показателем надежности служит характеристика эффективности затрат Эн на повышение надежности линии. Причем повышение надежности рассматривается как создание резерва, предоставляющего дополнительные возможности, сверх минимально необходимой для выполнения заданных функций
![]() (11)
(11)
где АН — повышение надежности в результате введения резерва; Зн — величина приведенных затрат на образование резерва.
Для оценки надежности может использоваться любой показатель.