- МАТЕМАТИЧЕСКАЯ МОДЕЛЬ НАДЕЖНОСТИ ЭЛЕМЕНТА
В литературе по теории надежности механических систем надежность определяется как вероятность того, что действующая на элемент нагрузка Q не превзойдет прочности элемента R:
![]() (102)
(102)
Выражения (102) называют математической моделью вероятности безотказной работы.
С точки зрения терминологии, принятой в электронике, зависимости (102) не совсем точно определяют вероятность безотказной работы, так как в них отсутствует элемент времени. В вероятность безотказной работы определяется как вероятность того, что отказ не возникает в пределах заданной наработки. Однако в дальнейшем авторы будут придерживаться избранного подхода.
Рассмотрим теоретическую модель подробнее. Нагрузка и прочность являются случайными величинами и описываются собственными функциями распределения (F(q) и F(r)) и плотностями распределения (f(q) и f(r)).
Вероятность превышения прочностью некоторого значения нагрузки q является по приведенному выше определению функцией распределения величины Q и может быть определена с помощью формулы
![]() (103]
(103]
Нагрузка и прочность являются величинами независимыми. Поэтому вероятность того, что значение нагрузки находится в бесконечно малом интервале dq, а прочность превышает эту нагрузку определяют по выражению
1![]() . (104)
. (104)
я
Проинтегрировав (104) по dq, можно получить вероятность того, что прочность элемента будет больше всех возможных значений нагрузки:
![]() (105)
(105)
Это выражение для определения вероятности безотказной работы элемента приведено во многих литературных источниках.
Аналогично может быть получено выражение для вероятности безотказной работы элемента в предположении, что нагрузка окажется меньше любого значения прочности:
![]() (106)
(106)
В некоторых случаях бывает необходимо определить не вероятность безотказной работы элемента, а обратную величину — вероятность отказа
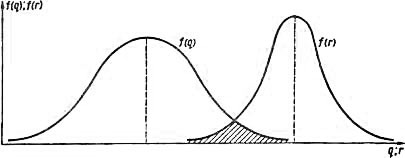
Рис. 6. Графическая интерпретация вероятности безотказной работы элемента
Рассуждая аналогично приведенному выше, получим
![]() (108)
(108)
Реально климатические нагрузки, так же как и прочность элементов, не могут иметь отрицательных значений, поэтому окончательно можно записать для вероятности безотказной работы
![]() (109)
(109)
и для вероятности отказа
![]() (110)
(110)
На рис. 6 приведена графическая интерпретация вероятности безотказной работы элемента. В общей системе координат изображены плотность распределения нагрузки f{q) и плотность распределения прочности /(г). Площадь заштрихованной области перекрытия кривых является численным решением формулы (110).
Полученные выражения для определения вероятности безотказной работы и вероятности отказа могут быть применены в автоматизированных системах проектирования, но требуют значительных затрат времени и огромной предварительной работы по сбору и обработке систематических данных о распределениях нагрузок и прочности элементов.
Данные о климатических нагрузках получают на основании обработки наблюдений на метеорологических станциях и специализированных метеорологических постах. Вопрос этот достаточно хорошо изучен и не представляет особых трудностей в системе получения необходимой информации.
Получить же необходимую информацию о распределениях прочности некоторых элементов ВЛ (в первую очередь конструкций опор) часто оказывается невозможным.
Распределение прочности железобетонных или металлических конструкций может быть получено теоретически, однако при этом не могут быть учтены особенности технологии производства, присущие каждому отдельному заводу, поэтому теоретические распределения могут значительно отличаться от реальных. Получение статистических данных, основанных на результатах заводских испытаний, привело бы к огромным материальным затратам, так как связано с разрушением очень большого количества готовых изделий.
Поэтому заводские испытания на прочность, например, железобетонных опор, предусматривают лишь оценку несущей способности готовых изделий. Если испытываемый контрольный образец выдерживает нагрузку, равную 1,4 расчетной, то испытания прекращаются, образец не доводится до разрушения и возвращается в партию готовых изделий.
Закон распределения климатической нагрузки зависит только от синоптических и физико-географических условий местности и невозможно каким-либо образом изменить его параметры. На параметры закона распределения прочности элемента можно влиять различными способами, например заменой материала, совершенствованием технологии изготовления и т.п. Таким образом, при каждом изменении в производстве любого элемента ВЛ необходимо заново собирать и обрабатывать статистический материал, чтобы получить распределение прочности. Такой путь оказывается трудоемким и дорогостоящим, а потому нецелесообразным.
Кроме того, чрезвычайно сложными оказываются математические модели, позволяющие описать изменение напряжений в материале рассматриваемого элемента при приращении нагрузки. С примерами таких моделей можно ознакомиться в литературе. В данной работе указанные модели рассматриваться не будут.
Для массовых расчетов имеет смысл использовать более простые методы, не требующие большой предварительной подготовки исходных данных. Простой и достаточно точный метод расчета надежности ВЛ при проектировании основан на двух предпосылках.
Первая предпосылка базируется на том, что на стадии проектирования нет необходимости определять точное значение надежности BЛ, достаточно получить результат, свидетельствующий о том, что действительный уровень надежности элемента не ниже полученной расчетной величины. Эта предпосылка дает возможность использовать вместо двух распределений (нагрузка и прочность) только одно. Вторая величина может быть задана детерминированным значением. Исходя из соображений, изложенных выше, представляется целесообразным детерминированным значением задавать прочность элемента.
Вторая предпосылка может быть сформулирована следующим образом: нагрузка не должна превышать значение, при котором напряжение в материале элемента равно предельно допустимому, т.е. значение нагрузки можно взять численно равным принятому значению прочности.

Рис. 7. Определение вероятности безотказной работы при детерминированном значении прочности элемента
Необходимо отметить, что аналогичный подход рекомендуется и к определению надежности ВЛ. Графическая интерпретация метода приведена на рис. 7. Здесь F(q) — функция распределения нагрузки, г — детерминированное значение прочности, Ps — вероятность безотказной работы.
Рассмотрим нагрузки меньше прочности элемента. Вероятность того, что значение нагрузки меньше некоторой величины др, описывается функцией распределения нагрузки
![]() (111)
(111)
Вид функции (111) определяется на основании обработки статистических данных метеорологических станций.
В показано, что при больших периодах наблюдений (более 10 лет) нет необходимости рассматривать все множество наблюдений. Достаточно рассмотреть только подмножество наибольших значений в принятых интервалах времени. Исходя из этого для описания закона изменения нагрузок во времени используется функция распределения их годовых максимумов, что позволяет с небольшим приближением считать, что наблюдения производятся через равные промежутки времени.
Появление интересующего нас события, заключающегося в том, что значение нагрузки будет равно q или превзойдет его, равновероятно в любом из наблюдений (испытаний). Отсюда следует, что для появления хотя бы одного такого события необходимо провести в среднем 1 /Р испытаний. Так как наблюдения (испытания) проводятся через равные промежутки времени, величина l/Pf является средним периодом времени, в течение которого нагрузка не превзойдет заданной величины. Величину 1 /Р. называют периодом повторяемости величины д и обозначают буквой Т. Из (111) следует, что
где qp — расчетная величина нагрузки.
Величина Р=1/Т в соответствии с может рассматриваться как средняя частота отказов со.
Из приведенных рассуждений следует, что наиболее простым и удобным показателем надежности является средняя частота отказов
![]()
(113)
Если функцию распределения нагрузки ограничить значением нагрузки, вызывающей в материале элемента предельно допустимые напряжения, превышение которых приводит к разрушению всех элементов в зоне действия этой нагрузки, то величина со будет характеризовать частоту массовых отказов отдельных элементов.
Анализ формул (112) и (113) показывает, что средняя частота (далее частота) отказов зависит только от вида распределения нагрузок и принятого периода повторяемости предельно допустимого значения нагрузки.
Рассмотренный выше показатель надежности — частота отказов — прост для расчетов и удобен для нормирования, однако является усредненной характеристикой и не позволяет получить ответ на один из основных вопросов надежности: с какой степенью уверенности можно гарантировать, что за срок службы линии не произойдет ни одного отказа (один, два и более отказов)?
Для получения ответа следует использовать другой показатель надежности — вероятность безотказной работы.
Для вывода математического выражения вероятности безотказной работы обратимся к аппарату с теории вероятностей, предварительно вспомнив два положения, изложенные выше.
Первое: значение F(qp) является обеспеченностью величины qp или вероятностью того, что эта величина не будет превышена. Второе: закон распределения F(q.) описывает распределение только годовых максимумов нагрузки, что позволяет идентифицировать понятия «период, равный одному году» и «одно испытание».
Вероятность того, что событие А произойдет m раз в течение п испытаний, подчиняется биноминальному распределению и определяется выражением
![]()
где N — срок службы линии, лет; m — количество отказов за срок службы линии.
Выразив F(q) через период повторяемости нагрузок, получим
(115)
Используя в (114) обозначения, принятые в настоящей работе, получим
![]()
(114)
![]() (116)
(116)
Из (116) можно получить вероятность хотя бы одного, двух и более отказов за срок службы линии. При этом необходимо учитывать, что срок службы линии должен быть меньше (в пределе равен) периода повторяемости предельно допустимых нагрузок, иначе формула (116) дает неверный результат. Это ограничение не относится к случаю, когда необходимо оценить вероятность безотказной работы.
Положив т - О, получим
![]() (117)
(117)
На практике для определения вероятности безотказной работы используется другое выражение, которое при TfN дает те же результаты, что и (117):
![]() (118)
(118)
В [69 J величину![]() называют риском принятого решения.
называют риском принятого решения.
Величина R определяет вероятность того, что за срок службы N нагрузка, имеющая период повторяемости Т, может быть превышена.
Оба рассмотренных показателя надежности — частота отказов и вероятность безотказной работы — определяются через период повторяемости нагрузок, поэтому каждый показатель может быть выражен через другой.
Подставив в (117) значение Т из (112), получим
(119)
или
![]() (120)
(120)
Последнее выражение позволяет утверждать, что вероятность безотказной работы подчиняется экспоненциальному закону.
В свою очередь, частота отказов может быть выражена через вероятность безотказной работы
![]() (121)
(121)
В разделе 2.2.1 говорилось о попытках оказывать влияние на надежность изменением периода повторяемости нагрузок. Из формул (112) и (117) следует, что период повторяемости нагрузок может характеризовать среднюю частоту отказов, являясь ее обратной величиной подобно тому, как частота и период колебаний являются обратными величинами.
Вероятность безотказной работы может быть охарактеризована периодом повторяемости предельно допустимых нагрузок только в сочетании со сроком службы линии.