Впервые статистическая природа запаса прочности (см. п. 2.1.1.) была показана в 1926 г. М. Майером и в 1929 г. Н. Ф. Хоциаловым. Последний, работая на крупнейшей для своего времени стройке «Свирь ГЭС», обратил внимание на неизбежный разброс кубиковой прочности бетона, укладываемого в тело плотины электростанции. Считая максимальную гидростатическую нагрузку на тело плотины детерминированной, а прочность бетона подчиняющейся нормальному закону распределения, он получил формулу для необходимого запаса прочности, гарантирующего неразрушаемость с заданной заранее обеспеченностью, достаточно близкой к единице. Статьи Н. Ф. Хоциалова значительно опередили представления того времени о коэффициенте запаса, трактовавшегося тогда многими как «коэффициент незнания», и поэтому прошли незамеченными широким кругом специалистов.
Существенным развитием вдей М. Майера и Н. Ф. Хоциалова явились работы Н. С. Стрелецкого, который исследовал совместно функции распределения нагрузки и несущей способности конструкции. Было введено понятие гарантии неразрушимости Г, т.е. верхней оценки безотказной работы элемента,
![]() (12)
(12)
где а>у — вероятность того, что фактическая несущая способность получит значение меньшее, чем расчетное значение R0; а>2 — вероятность того, что нагрузка получит значение, превосходящее расчетную величину Q0.
Впоследствии была дана нижняя граница неразрушимости:
![]() (13)
(13)
Оценки надежности Г и Гн не зависят от вида функции распределения, легко вычисляются и были использованы при создании норм проектирования.
Хотя Н. С. Стрелецкому не удалось найти математически правильного решения задачи о связи между коэффициентом запаса и кривыми распределения нагрузок и прочности, тем не менее его работы сыграли важную роль в постановке проблемы надежности строительных конструкций и пропаганде статистических методов расчета. Именно они послужили началом развития нового раздела теории расчета сооружений — теории надежности строительных конструкций.
А. Р. Ржаницин ввел предположение о нормальном распределении несущей способности R и нагрузки Q и определил функцию неразрушимости гр следующим образом:
![]() (14)
(14)
В этом случае надежность конструкции оценивается с помощью характеристики безопасности
![]() (15)
(15)
где E(R), E(Q) — математические ожидания соответственно несущей способности конструкции и действующих на нее нагрузок; v — коэффициент вариации.
При увеличении у надежность возрастает. В частности, для у = 3 вероятность безотказной работы Ps = 0,9987. Ограничением к использованию метода оценки по А. И. Ржаницину является исходное допущение о виде функции распределения нагрузки. Поскольку основным видом силового воздействия на опоры ВЛ и порталы ОРУ являются ветровые и гололедные нагрузки, функции распределения которых обладают ярко выраженной асимметрией, они не могут быть заменены нормальным распределением.
А. И. Ржанициным были даны также рекомендации по учету повторяемости загружений и учету совместной работы элементов конструкций, в частности, при параллельном и последовательном их соединении. Для сложных нелинейных детерминированных соотношений рекомендовался метод вероятностной линеаризации.
Аналогичные исследования также проведены и опубликованы за рубежей А. М. Фрейденталем, Р. Леви и др..
Обосновал общие принципы построения теории надежности и разработал методы решения основных задач надежности механических систем В. В. Болотин. Разработанная им теория базируется на описании нагрузок и несущей способности конструкции с помощью случайных процессов. Изменение несущей способности во времени определяется с учетом накопленных повреждений. Понятие отказа определяется как случайный выброс из области допустимых состояний. Общий метод расчета надежности, предложенный Болотиным, построен на применении теории случайных процессов. Поэтому прямое его использование ограничивается сложностью математического аппарата и недостатком исходной статистической информации о базисных переменных.
Поскольку надежность строительных сооружений достаточно высока, В. В. Болотин предложил оценивать уровень надежности в логарифмических единицах (белах):
![]() (16)
(16)
где Pf — вероятность наступления за срок службы конструкции хотя бы одного отказа; Ps — вероятность безотказной работы.
Показателю надежности Ps= 0,9 соответствует уровень р = 1Б, показателю надежности Ps = 0,99 — уровень р = 2Б и т.д.
Аналитическое решение
Совокупность базисных переменных, определяющих надежность сооружения, представляется случайным вектором:
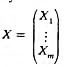 (17)
(17)
Базисные переменные целесообразно рассматривать в m-мерном пространстве, каждая точка которого есть одна реализация случайного вектора X.
Функцию распределения наименьших значений называют также распределением Вейбулла. Это распределение использовано для описания скоростей ветра на территории бывшего СССР и нормирования ветровых нагрузок на здания и сооружения.
К типу III приводят исходные распределения, которые имеют в направлении экстремального значения границу х0 и могут быть представлены в окрестностях этого значения степенным рядом.
Для определения нагрузок на электросетевые конструкции МЭК рекомендует использовать первый тип распределения.
Обработка данных более 200 метеостанций Украины показала следующее.
- Распределения Гумбеля, Фишера-Типпетта и Вейбулла аппроксимируют данные наблюдений практически равноценно в области малых периодов повторяемости (5, 10 и 25 лет), т.е. замена одного типа распределения другим не может существенно повлиять на результаты оценки надежности.
- Значения климатических нагрузок, вычисленных для больших периодов повторяемости (50—500 лет), существенно различаются в зависимости от типа используемого распределения. Для распределений первого и третьего типов разница составляет в среднем 15%. Величины нагрузок, вычисленные с использованием второго типа распределения, завышены в среднем на 40%, а в отдельных случаях — более чем на 100%. При этом метеорологические параметры достигают значений не свойственных данной местности, а нередко и данному параметру.
Поскольку при решении задач по обеспечению требуемого уровня надежности необходимо иметь достоверную информацию именно для областей редких повторяемостей, данное обстоятельство не позволяет рекомендовать распределения типа II для описания климатических нагрузок. - Для отдельных метеостанций наилучшая аппроксимация различных видов нагрузок достигается при использовании разных типов распределений. То есть выбор вида функции является задачей, не имеющей однозначного решения. При описании нагрузок на строительные конструкции часто используют и другие типы распределений: экспоненциальное, нормальное, логарифмически нормальное, гамма-распределение (табл. 2).
Серьезную проблему представляет собой получение сочетания вероятностей коррелированных переменных. Поэтому на практике часто применяют упрощенный метод: низкая вероятность появления одной переменной принимается в сочетании с высокими вероятностями остальных переменных.
2.2. Виды распределений
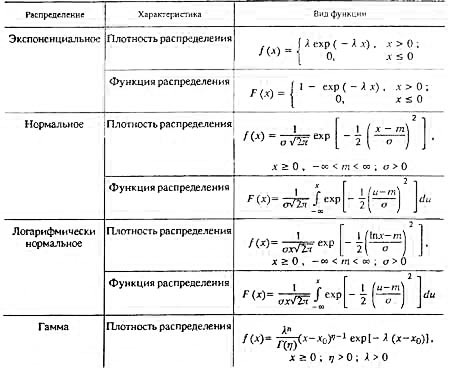
Распределение | Характеристика | Вид функции |
| Функция распределения |
|
Экстремальных значений типа I | Плотность распределения наибольших значений |
|
То же, наименьших значений |
| |
Функция распределения наибольших значений |
| |
То же, наименьших значений |
| |
Экстремальных значений типа II | Плотность распределения наибольших значений |
|
То же, наименьших значений |
| |
Функция распределения наибольших значений |
| |
То же, наименьших значений |
| |
Экстремальных значений типа III | Плотность распределения наибольших значений |
|
То же, наименьших значений |
| |
Функция распределения наибольших значений |
| |
То же, наименьших значений |
|
Трудно поддаются статистическому описанию различного рода колебания проводов (эолова вибрация, пляска проводов, колебание пучка проводов между распорками, вибрация в турбулентном потоке, подскок проводов при сбросе гололедных отложений и пр.). Не исключена и возможность попадания отдельных участков ВЛ в зоны, где микроклимат существенно отличается от общих условий климатического района. Для таких зон данные наблюдений часто полностью отсутствуют.
В работах В. В. Болотина отмечено, что природные нагрузки следует описывать не просто случайными величинами, а случайными процессами. Описание процесса будет тем точнее, чем выше порядок задаваемой функции распределения. Однако, с одной стороны, имеющаяся статистическая информация не позволяет задавать порядок распределения выше второго, с другой, — если считать, что надежность конструкции определяется редкими экстремальными значениями нагрузок, то при описании распределения таких нагрузок их значения можно считать статистически независимыми.
Несущая способность сооружения или его элемента может быть определена на основании законов сопротивления материалов, строительной механики, теории упругости и пластичности как функция различных геометрических и физических параметров конструкции, многие из которых являются случайными величинами или случайными процессами.
Определенные трудности при вычислении показателей надежности представляет учет изменения несущей способности сооружения во времени. Основными факторами, влияющими на изменение прочности электросетевых конструкций, является коррозионный износ элементов и узлов и накопление повреждений в процессе эксплуатации.
Особенностью работы металлических опор ВЛ и порталов ОРУ под нагрузкой является внецентренное сжатие стержней конструкции, что объясняется наличием жестких узлов, расцентровкой осей стержней в узловых соединениях, необходимостью воспринимать внеузловые нагрузки и пр. В сочетании с большой гибкостью стержней указанные особенности существенно повышают вероятность получения стержнями случайных погнутостей и других отклонений.
В то же время высокая степень статической неопределимости конструкций приводит к проявлению принципа резервирования и, следовательно, к увеличению надежности. Повышает надежность конструкции и способность металла к пластическим деформациям.
Для железобетонных электросетевых конструкций характерны существенные отклонения оси стоек от вертикали, зависящие от качества заделки в грунт и создающие дополнительные усилия в конструкции. Несущую способность железобетонных конструкций существенно снижает также применение некачественных бетонов и нарушение технологии армирования. Указанные особенности необходимо учитывать при отыскании плотности распределения несущей способности сооружения.
В работе для определения вероятности безотказной работы элемента конструкции использован следующий подход. В элементе конструкции, для которого вычисляется показатель надёжности, результирующее усилие представляется в виде суммы слагаемых
N = 7VX + N2 + N3, (53)
где N1, N2, N3 — усилия соответственно от собственного веса элементов конструкции, ветровых нагрузок и гололедных нагрузок.
В свою очередь каждое слагаемое вычисляется по формуле
![]() (54)
(54)
где jt — номер точки приложения нагрузки /; mi — число точек приложения нагрузки /; FtJ — величина нагрузки в точке у; Кц — коэффициент, численно равный величине усилия в рассматриваемом элементе от единичной силы, приложенной в точке у.
Для описания составляющих N2, N3 усилия N использованы распределения Вейбулла и Фишера-Типпета. Случайная величина N1 описывается нормальным законом.
Несущая способность R элемента описывается функциональной зависимостью R=f(X'•), в которой Xj (z=l ...п) — случайные компоненты, характеризующие прочность материала и геометрию сечения элемента. Несущая способность
![]() (55)
(55)
где Ry — сопротивление материала элемента; А — площадь сечения элемента; <р — коэффициент продольного изгиба (неслучайный параметр); ус — коэффициент условий работы конструкции (неслучайный параметр).
Математическое ожидание и дисперсия функции плотность распределения fR (Л) величины R определяется с помощью приближения функции fR рядом Тейлора. Такой метод дает точный результат,только когда все частные производные второго и более высоких порядков равны нулю. Применимость этого метода ограничена функциями, для которых разложение в ряд Тейлора не слишком громоздко. Условие безотказности записывается в виде
![]() (56)
(56)
или
![]() (57)
(57)
где Z — случайная величина, распределенная нормально,
![]() ; (58)
; (58)
E(Z), E(R), E(Nl) — математическое ожидание соответственно Z, R, Nt; V(Z), V(R), V(NJ - дисперсии Z, R, Nv
Вычисление вероятности безотказной работы проводится для двух расчетных условий.
1. Гололед отсутствует (N3 = 0). Тогда вероятность безотказной работы можно определить по формуле
![]()
где fN2 — плотность распределения величины ветровой составляющей
усилия в элементе.
- Режим гололеда (N3 не 0). В этом случае скоростной напор ветра принимается постоянным и равным 0,25 максимального нормативного напора. Вероятность безотказной работы определяется по формуле
![]()
где N'2 — составляющая усилия в элементе, вызванная давлением ветра интенсивностью q; fN^ — плотность распределения величины гололедной
составляющей усилия в элементе.
За последние 15—20 лет в США была разработана методика расчета опор ВЛ с использованием теории вероятностей. В основу этой методики положены следующие принципы:
- линия электропередачи состоит из отдельных взаимосвязанных элементов (опор, фундаментов, проводов, арматуры);
- изменения климатических нагрузок носят случайный характер;
- в расчете используются предельные (без коэффициента надежности) нагрузки, превышение которых приводит к аварии;
- расчетные предельные нагрузки определяются с учетом результатов экономического обоснования принимаемых проектных решений;
- в расчетах принимается заранее заданная последовательность разрушения отдельных элементов линии.
Для конструкций, рассчитанных с использованием этой методики, возможность аварий полностью не исключается. Это объясняется тем, что строительство электросетевых конструкций, способных воспринять любые климатические нагрузки, экономически нецелесообразно.
Для оценки надежности воздушной линии электропередачи в целом существуют различные формулировки функции надежности Si 1). В частности, этот показатель может быть определен по формуле
![]()
(62)
где P. (t) — вероятность нахождения линии в момент времени t в состоянии i; (2, (0 — вероятность нарушения надежности линии в момент времени t в состоянии г.
Формула (62) одинаково характеризует все нарушения независимо от их природы и значимости. Учет указанных факторов может быть осуществлен введением коэффициента значимости нарушения работоспособности:
![]() (63)
(63)
где W — коэффициент значимости нарушения ВЛ, который зависит от относительной длительности восстановления работоспособности линии, величины ущерба и пр.
Выражение (63) используется для расчета условного показателя надежности системы.
Во многих странах (США, Канаде, Германии, Австралии) при проектировании ВЛ выбор оптимального варианта линии производят путем сравнения различных вариантов ее конструктивного решения и затрат, связанных с обеспечением надежности. В качестве показателя надежности воздушных линий электропередачи принимают вероятность отказа или повреждения ее элемента. Для определения вероятности Pf повреждения элемента линии необходимо знать функции распределения нагрузок, воспринимаемых элементом линии, и прочности этого элемента. Расчет выполняют по формуле (35).