Лекція 11
Розрахунок сталого режиму складно-замкнених мереж методом перетворення
План
1. Еквівалентування паралельних ліній при відсутності на них навантаження.
2. Перенос навантажень в інші точки мережі.
3. Перетворення трикутника в еквівалентну зірку.
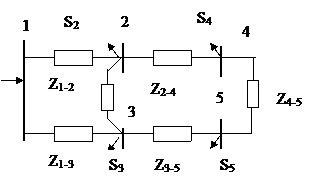Суть методу перетворення мережі складається в тому, що задану складну мережу шляхом поступових перетворень призводять до мережі з двостороннім живленням. Потім, після визначення потужностей на кожній ділянці перетвореної схеми, за допомогою зворотних перетворень знаходять дійсний розподіл потужностей у вихідній схемі мережі.
Розбір за допомогою студентів такої мережі:
Питання: Які перетворення потрібні для цієї мережі?
Питання: Як розрахувати режим мережі, що утворилася.
1. Еквівалентування паралельних ліній при відсутності на них навантаження.
Суть задачі:
- є ділянка мережі з двома або декількома рівнобіжними лініями, що мають опори Z1, Z2…(рис. 1);
- потрібно замінити ці лінії одною еквівалентною з опором Zекв і навантаженням Sекв за умови, щоб напруга у вузлі В залишилися при перетворенні незмінною.
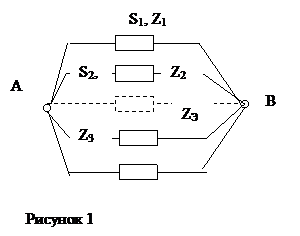Для двох ліній маємо:
Sекв =S1+S2; Zекв = Z1||Z2
Для трьох ліній маємо:
Sекв =S1+S2+S3;
Zекв =1/(1/Z1+1/Z2+1/Z3)
При зворотному перетворенні до вихідної схеми потрібно знайти розподіл Sекв по вітках вихідної мережі. За умовою задачі напруга у вузлі В повинна бути незмінною, тому і падіння напруги на лініях повинні бути однаковими:
.
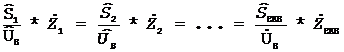Знайдемо:
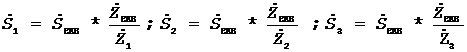
2. Перенос навантажень в інші точки мережі.
Коли виникає необхідність у переносі навантажень у вузли мережі? Роздивимося мережу (рис. 2) із двостороннім живленням. Тому що на лініях є навантаження, то падіння напруги в лініях різноманітні і еквівалентувати їх не можна. Для того, щоб зробити еквівалентну заміну паралельних ліній, що мають зосереджені навантаження, удаються до переносу навантажень в інші точки мережі.
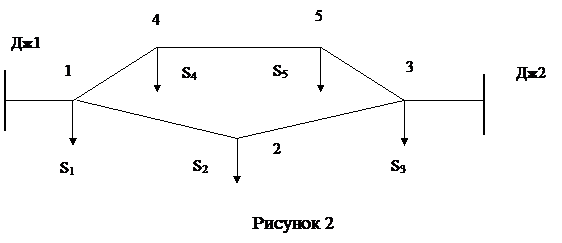У аналізованій мережі необхідно перенести навантаження в точках 4, 5, 2 у вузли 1 і 3.
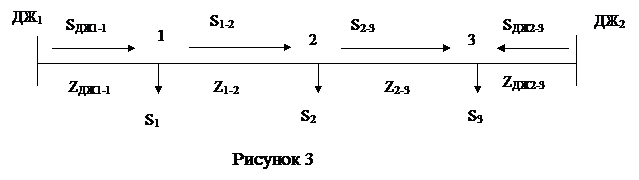
Припустимо, що потрібно замінити лінію 1-2-3 і лінію їй паралельну. Роздивимося 1-2-3. Вимоги до перетворення: навантаження, яка підключене до вузла 2, потрібно замінити двома еквівалентними навантаженнями SП2-1 і SП2-3, розташованими в точках 1 і 3 за умови, щоб потужності SДЖ-1 , SДЖ2-3 , на сусідніх ділянках і напруги в точках 1 і 3 як у вихідній, так і перетвореній схемах залишилися незмінними (рис. 3).
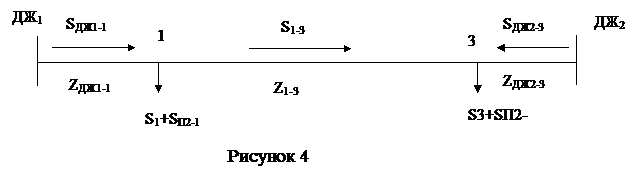
Припустимо, що точка потокорозподілу знаходиться у вузлі 3. За умовою задачі, падіння напруги на ділянці мережі 1-3 як у вихідній (рис. 3) так і перетвореній схемах (рис. 4) повинні бути однакові.
Питання для студентів: як найти струм по номінальній напрузі, як знайти падіння напруги.
Питання для студентів: записати другий закон Кірхгофа для ділянки 1-3:
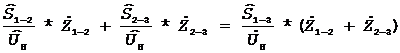(1)
По балансу навантажень у точках 1 і 2 без урахування втрат потужності маємо:
S1-2 =SДЖ1-1 – S1, S2-3 = S1-2 –S2 =SДЖ1-1 –S1 – S2 ; S1-3 =SДЖ1-1 –S1 – SП2-1 (2)
Після перетворень (1) з урахуванням (2) маємо:
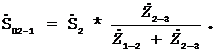
Подібним чином одержемо співвідношення і для переносу потужності з точки 2 у точку 3
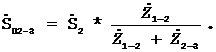
Висновок: перенесені навантаження визначаються за правилом, яке застосовується при визначенні потужностей на головних ділянках мережі з двостороннім живленням.
Зворотне перетворення: S1-2 =S1-3 + SП2-1.
Потужність на ділянці 1-3 у перетвореній схемі. Потужність на ділянці 1-2 вихідної схеми, після повернення в вузол 2 при позначеному на схемі напрямку потужностей, буде більшим потужності S1-3 на розмір потужності що повертається:
S2-3 =S1-3 - SП2-3 потужність на ділянці 2-3 після повернення в точку 2 буде меншим S1-3 на розмір потужності що повертається.
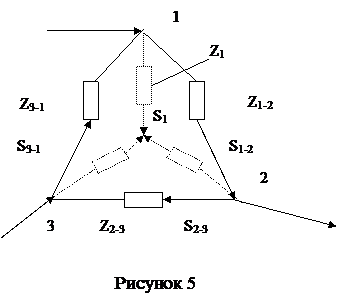
3. Перетворення трикутника в еквівалентну зірку.
Розглянемо трикутник без зосереджених навантажень на сторонах (рис. 5). Опори зірки, яке виникне як наслідок перетворень (рис. 5) визначаються з допомогою рівнянь
.
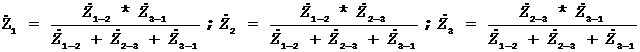Після визначення потужностей у перетвореній мережі знаходять потужності в гілках зірки S1 , S2 , S3 перетвореної схеми.
При перетворенні схеми у вихідну (зворотне перетворення) необхідно знайти розподіл потужностей в гілках трикутника на підставі отриманого розподілу потужностей в гілках еквівалентної зірки. При напрямках потужностей, які наведено на рис. 5 і номінальній напрузі маємо рівняння
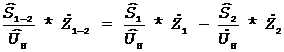. (3)
З (3) маємо
,
,
.
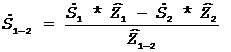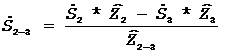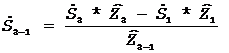Якщо отримаємо результат з негативним знаком, то це означає, що умовно прийнятий напрямок потужностей в гілці трикутника треба змінити на зворотний.