Бутырин П.А., Алпатов М.Е. (МЭИ, ОАО ХК «Электрозавод», Москва)
Надежность работы силовых трансформаторов в значительной степени определяет надежность работы любой электроэнергетической системы. В последнее время актуальность данной проблемы еще больше обострилась в связи с существенным возрастанием числа трансформаторов, отслуживших свой нормативный срок или близких к этому. Опасность возрастания аварийности оборудования в этих условиях определяет резкое повышение роли технической диагностики, как важнейшего инструмента обеспечения функциональной надежности трансформаторов. Можно констатировать, что сейчас эффективность диагностики трансформаторов явно недостаточна. Причиной этого является разрыв, образовавшийся между уровнем развития технических средств диагностики и ее теоретическим обеспечением. Под последним понимается разработанность моделей, в первую очередь математических, и, как следствие, разработанность аппарата обработки диагностической информации. Указанный разрыв наглядно выражается в слабой корреляции множеств диагностических параметров тестовой и функциональной диагностики, что затрудняет постановку диагноза.
Одними из наиболее информативных показателей состояния трансформаторов являются их электромагнитные параметры (параметры холостого хода, короткого замыкания, активные и индуктивные сопротивления и др.). Однако насущная задача контроля этих величин под нагрузкой не имеет до настоящего момента удовлетворительного решения. В настоящей работе показаны имеющиеся возможности для такой диагностики.
В качестве диагностической модели предлагается использовать описание трансформатора как четырехполюсника - модели, отличающейся точностью и минимальной размерностью при высокой информативности. В качестве электромагнитных параметров здесь рассматриваются элементы матриц Z - и Y - параметров эквивалентного четырехполюсника (многополюсника), а также их возможные комбинации. Можно показать, что все традиционные электромагнитные показатели (параметры электромагнитных испытаний), могут быть найдены с помощью указанных матриц.
Особенностью используемых моделей является их нелинейность. Отсюда следует, что для матриц Z0 и Yc, сформированных по данным соответственно двух опытов холостого хода (Z0) и двух опытов короткого замыкания (Yc) при номинальных воздействиях, не выполняется условие Z0 = Ycl, то есть эти матрицы описывают два разных объекта (два разных состояния одного объекта). Данное обстоятельство не учитывается в современной теории трансформаторов, поэтому традиционная схема замещения с параметрами, определенными по данным опытов холостого хода и короткого замыкания неадекватна реальному устройству и является результатом компромисса между данными двух несогласованных режимов (псевдорешение). Были проработаны вопросы согласования данных разных тестовых режимов. Обосновано, что в первом приближении такое согласование может быть осуществлено с помощью комплексного коэффициента х (коэффициента нелинейности):
Z=xZj,
xY=Yj,
где Zm, Ym (m = i, j) - матрицы Z и Y, составленные по данным m - го режима. Разработан алгоритм определения коэффициента х в различных режимах и в условиях различного объема информации.
Сформулирована задача определения электромагнитных параметров трансформаторов по рабочим токам и напряжениям [1]. В качестве диагностических моделей (как и в случае тестовой диагностики) предложено
также использовать объединенные уравнения состояния трансформатора в разных режимах:
U = ZI;
YU = I;
U = {U} 22 ; I = {I/} 22; Z = {Z4} 22; Y = {Y,^; Zri = R, + (w,/wJ)Rm +jcoL,; Zy = Rn = jcoM, где U-*, I/ - напряжение и ток i -ой обмотки трансформатора в j -м режиме (i, j = 1,2); соМ - взаимные активное и индуктивное сопротивления между обмотками; Ri9 wL - активное и индуктивное сопротивления i -ой обмотки (1=1, 2); w* - число витков i -ой обмотки (i = 1, 2). Выполнен анализ обусловленности систем уравнений функциональной диагностики на основе методов теории возмущений. Установлена плохая обусловленность указанных уравнений. Получены аналитические выражения для чисел обусловленности (для 1-х норм) матриц, входящих в диагностические модели. Разработан алгоритм выбора наилучшей модели.
Существенная нелинейность самого трансформатора, а также другие причины приводят к появлению высших гармоник в кривых токов и напряжений обмоток. В этих условиях становятся формально неприменимыми диагностические модели и методы диагностики, основанные на комплексном представлении. Исследованы возможности решения диагностических задач в условиях несинусоидальности, основанные на разработанном академиком Демирчяном К.С. методе ортогональных временных координат [2]. Можно показать, что указанный метод позволяет сохранить работоспособность комплексных моделей если в качестве модулей и фаз переменных использовать величины:
![]()
скалярное произведение векторов; А, В = Uj5 ; a, b = Uj, ij j=l, 2 .
С учетом плохой обусловленности используемых описаний трансформаторов исследована применимость для целей диагностики упрощенных математических моделей трансформаторов
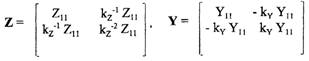
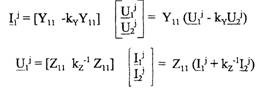
связанных с представлением последних как двухполюсников:
Проанализирован вопрос осуществления непрерывного мониторинга электромагнитных параметров трансформаторов на основе комбинации точных, но более медленных методов и быстрых, но требующих большей априорной информации, упрощенных методов диагностики.
Рассмотрены особенности диагностики многообмоточных и многофазных трансформаторов, в качестве основы для построения диагностических моделей которых используются уравнения состояния эквивалентных многополюсников.
Таким образом, проведенные исследования полностью подтверждают эффективность использования аппарата теории электрических цепей для диагностики электромагнитных параметров трансформаторов под нагрузкой.
Литература
- Бутырин П.А., Алпатов М.Е. Непрерывная диагностика трансформаторов/ Электричество. 1998. № 7. С.45-53.
- Демирчян К.С. Реактивная мощность на случай несинусоидальных функций. Ортомощность // Изв. РАН. Энергетика. 1992. №1. С. 15-38.